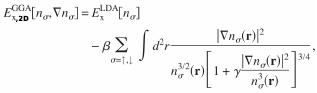Electronic Structure
From DFT foundations to excitonic effects in Nanowires
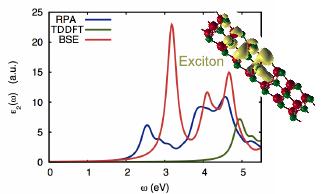
This research line was centered in a manifold of electronic structure methods. In particular, it followed two main axes: theory/code development and application of these methods to systems of interest. Concerning the method development, I have derived the exact conditions obeyed by the exchange and correlation functional for a non-uniform 2D-electron gas. Using these conditions I have then derived the 2D analogs of the most popular Density-Functional-Theory functionals (PBE, Becke functionals family[B88, B86 and MB86], Colle & Salvetti). Following the theoretical derivation, I also implemented these functionals in a widespread distributed library of exchange and correlation functionals, the LibXC. This has enabled DFT to accurately describe non-homogeneous 2D-electron gas present in systems as: modulated semiconductor layers and surfaces, quantum Hall systems, spintronic devices, among others. Concerning the applications, we used a broad spectrum of state-of-the-art ab-initio methods to study the electronic quantum confinement effects (in systems form 1 to 3-dimension: Nanowires, Quantum-Dots and Transparent-Conducting-Oxides). The methods employed to study these systems were: DFT and GW for the electronic structure; Density Functional Perturbation Theory to access determine phonon dispersions; Random-Phase-Approximation, Time-Dependent-DFT and Bethe-Salpeter equation to determine the optical properties. Of particular relevance was our work on Excitonic effects in the optical properties of nanowires. There we show for the first time how indispensable is the inclusion of local-field and excitonic effect to describe quantitatively the optical response of nanowires. We show that calculations based on the Fermi’s golden rule will never be able to catch the physics arising from the low dimensionality of the system, which is at the heart of the properties of Nanowires.This research line was centered in a manifold of electronic structure methods. In particular, it followed two main axes: theory/code development and application of these methods to systems of interest. Concerning the method development, I have derived the exact conditions obeyed by the exchange and correlation functional for a non-uniform 2D-electron gas. Using these conditions I have then derived the 2D analogs of the most popular Density-Functional-Theory functionals (PBE, Becke functionals family[B88, B86 and MB86], Colle & Salvetti). Following the theoretical derivation, I also implemented these functionals in a widespread distributed library of exchange and correlation functionals, the LibXC. This has enabled DFT to accurately describe non-homogeneous 2D-electron gas present in systems as: modulated semiconductor layers and surfaces, quantum Hall systems, spintronic devices, among others. Concerning the applications, we used a broad spectrum of state-of-the-art ab-initio methods to study the electronic quantum confinement effects (in systems form 1 to 3-dimension: Nanowires, Quantum-Dots and Transparent-Conducting-Oxides). The methods employed to study these systems were: DFT and GW for the electronic structure; Density Functional Perturbation Theory to access determine phonon dispersions; Random-Phase-Approximation, Time-Dependent-DFT and Bethe-Salpeter equation to determine the optical properties. Of particular relevance was our work on Excitonic effects in the optical properties of nanowires. There we show for the first time how indispensable is the inclusion of local-field and excitonic effect to describe quantitatively the optical response of nanowires. We show that calculations based on the Fermi’s golden rule will never be able to catch the physics arising from the low dimensionality of the system, which is at the heart of the properties of Nanowires. Below, you can find the most relevant works of our group.
Publications
J. G. Vilhena, E. Räsänen, M. A. L. Marques and S. Pittalis. “Construction of the B88 exchange-energy functional in two dimensions“. Journal of Chemical Theory and Computation 10, 1837 (2014).

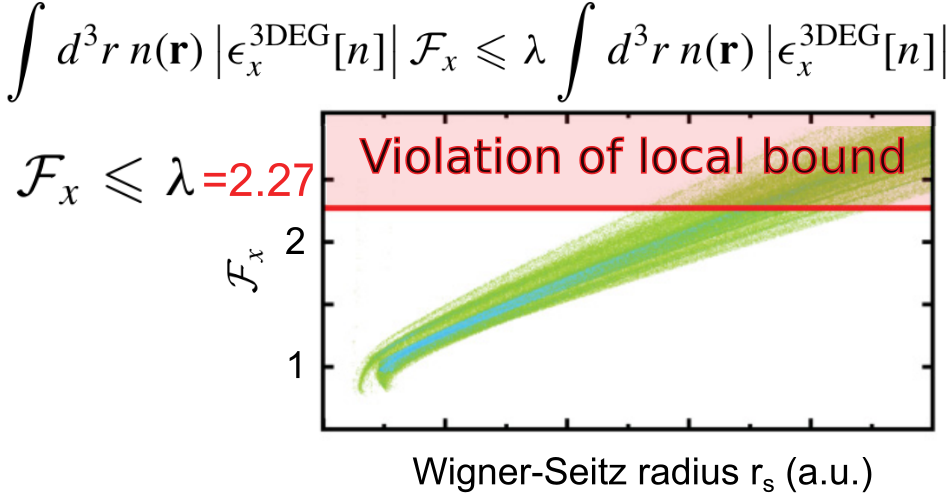
J. G. Vilhena, E. Räsänen, L. Lehtovaara and M. A. L. Marques. “Violation of a local form of the Lieb-Oxford bound“. Physical Review A 85 (5), 052514 (2012).
A. Putaja, E. Räsänen, R. van Leeuwen, J. G. Vilhena and M. A. L. Marques. “Kirzhnits gradient expansion in two dimensions“. Physical Review B 85 (16), 165101 (2012).

E. Räsänen, S. Pittalis, J. G. Vilhena and M. A. L. Marques. “Semi‐local density functional for the exchange‐correlation energy of electrons in two dimensions“. International Journal of Quantum Chemistry 110 (12), 2308 (2010).
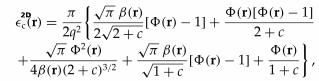
J. G. Vilhena, S. Botti and M. A. L. Marques. “Excitonic effects in the optical properties of CdSe nanowires”. Applied Physics Letters 96 (12), 123106 (2010).
S. Pittalis, E. Räsänen, J. G. Vilhena and M. A. L. Marques. “Density gradients for the exchange energy of electrons in two dimensions“. Physical Review A 79 (1), 012503 (2009).